#알고리즘
- 알고리즘이란?
▪ 알고리즘이란 문제를 해결하는 최선의 선택.
▪ 컴퓨터가 문제의 답을 찾아나가는 방법은 수없이 많으나, 코드를 구성하는 방법은 매우 많다.
▪ 어떤 코드가 가장 효율적일지 문제의 유형마다 최선의 방식을 학습하는 것이 필요.
#탐욕 알고리즘(Greedy)
- 탐욕 알고리즘이란?
▪ 선택의 순간마다 당장 눈앞에 보이는 최적의 상황만을 쫓아 최종적인 해답에 도달하는 방법.
▪ 탐욕 알고리즘의 단계는 다음과 같이 나눌 수 있다.
① 선택 절차(Selection Procedure): 현재 상태에서의 최적의 해답을 선택
② 적절성 검사(Feasibility Check): 선택된 해가 문제의 조건을 만족하는지 검사
③ 해답 검사(Soultion Check): 원래의 문젝제가 해결되었는지 검사 후, 아니라면 선택 절차로 돌아가 위의 과정을 반복.
- 탐욕 알고리즘의 조건
▪ 탐욕 알고리즘은 특정 상황에서만 최적의 해를 보장한다.
① 탐욕적 선택 속성(Greedy Choice Property): 앞의 선택이 이후의 선택에 영향을 주지 않음.
② 최적 부분 구조(Optimal Substructure): 문제에 대한 최종 해결 방법이 부분 문제에 대한 최적 문제 해결 방법으로 구성.
#완전 탐색 알고리즘(Brute-Force Algorithm)
- 완전 탐색 알고리즘이란?
▪ BFA 즉, 완전 탐색 알고리즘은 모든 가능성을 시도하여 해답을 찾아낼 때까지 반복하는 알고리즘이다.
- 완전 탐색 알고리즘의 사용
▪ 완전 탐색 알고리즘은 다음과 같은 경우에 사용된다.
① 프로세스 속도를 높이는 데 사용할 수 있는 다른 알고리즘이 없음
② 문제를 해결하는 여러 솔루션을 각각 확인해야 할 때.
▪ BFA의 단점은 시간복잡도이다. BFA는 O(n)의 시간복잡도를 가지기 때문에 데이터의 범위가 커질 수록 비효율적이다.
따라서 데이터의 규모가 적당한 경우에만 BFA를 사용하고, 이보다 커질 경우 정확하지 않더라도 다른 알고리즘을 통해 문제를 해결한다.
▪ 대표적인 완전탐색 알고리즘은 다음과 같다.
① 순차 검색 알고리즘 (Sequential Search)
: 배열 안에 특정 값이 존재하는지 검색 시, 인덱스 0부터 마지막 인덱스까지 검색.
public boolean cotains(int[] arr, int k) {
boolean result = false;
for (int i = 0; i < arr.length; i++) {
if (arr[i] == k) result = true;
}
return result;
} // 모든 값을 순회하여 해당 값의 존재 여부를 리턴.
② 문열 매칭 알고리즘 (Brute-Force String Matching)
: 길이가 n인 전체 문자열이 특정 문자열 m을 포함하는지 검색
public boolean BFSM(String[] arr, String[] targetArr) {
int n = arr.length;
int m = targetArr.length;
boolean result = false;
for (int i = 0; i <= n - m; i++) {
int j = 0;
while (j < m && targetArr[j].equlas(arr[i + j})) {
j++;
}
if (j == m) result = true;
}
}
return result;
}
③ 선택 정렬 알고리즘 (Selection Sort)
: 전체 배열을 오름차순/내림차순으로 정렬함.
public int[] arrSort(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
int min = i;
for (int j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[min]) min = j;
}
int tmp = arr[i];
arr[i] = arr[min];
arr[min] = tmp;
}
return arr;
}
④ 버블 정렬 알고리즘(Bubble sort)
: 서로 인접한 두 원소를 검사하여 정렬하는 알고리즘, 선택 정렬과 기본 개념이 유사함.
public int[] bubbleSort(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
for (int j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[i]) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = arr[i];
}
}
}
return arr;
}
⑤ Tree 자료 구조의 완전탐색 알고리즘 - Exhausive Search (BFS, DFS)
⑥ 동적 프로그래밍 DP(Dynamic Programing)
: 하나의 문제를 여러 개의 작은 문제로 나누어 결과값을 저장한 뒤 큰 문제를 해결할 때 사용하는 프로그래밍 방법.
#이진 탐색 알고리즘(Binary Search Algorithm)
- 이진 탐색 알고리즘이란?
▪ 이진 탐색 알고리즘은 데이터가 정렬된 상태에서 절반씩 범위를 나눠 분할 정복기법으로 특정한 값을 찾아내는 방법.
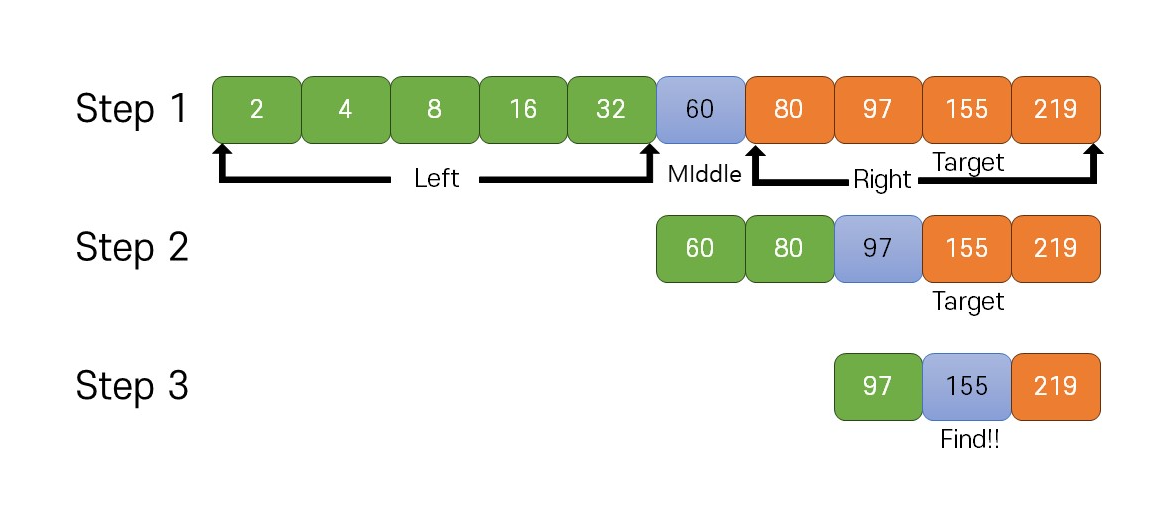
▪ 이진 탐색 알고리즘의 단계는 다음과 같다.
① 정렬된 배열의 가장 중간 인덱스를 지정
② 찾으려고 하는 값이 지정한 중간 인덱스의 값이면 탐색 종료.
③ 찾으려는 값이 인덱스의 값을 기준으로 큰 값인지, 작은 값인지 확인.
④ 값이 있는 부분과 값이 없는 부분으로 분리
⑤ 값이 있는 부분에서 다시 1단계로 돌아가 반복
▪ 이진 탐색 알고리즘은 주로 다음과 같은 경우에 사용된다.
① 정렬된 배열에서 요소값을 더 효율적으로 검색할 때
② 정렬된 데이터의 양이 많을 때 (데이터의 양이 많으면 많을수록 더 효율적: 시간복잡도 O(logn))
▪ 다음과 같은 제한사항도 있다.
① 배열에서만 구현 가능
② 정렬되어 있어야 구현 가능
'개발지 > Today I learn' 카테고리의 다른 글
| [1212] 자바 스프링 - Spring MVC (0) | 2023.12.12 |
|---|---|
| [1208] 자바 스프링 - Spring Framework (3) | 2023.12.08 |
| [1204] 자바 - 시간복잡도(Time Complexity) (2) | 2023.12.04 |
| [1128] 자바 - Tree traversal(트리 순회) (1) | 2023.11.28 |
| [1128] 자바 - Graph (그래프) (2) | 2023.11.28 |


